When Does Learning Work? Or When Can We Expect the Robot Uprising?

In my secret laboratory, I have created, perhaps, the greatest robot known to humanity! It runs, swims, flies, and makes delicious sandwiches. Well, it would, but it keeps falling over. 

Aha! This robot will learn to move! (Downloads reinforcement learning package.) And… it… doesn’t… work… (Two weeks of frantic grad students later.) My creation is alive! Oh, it fell again. There it goes, back up and running! Good robot!

This scenario plays out repeatedly in the world of control. From superhuman gameplay to self-driving cars, learning approaches have changed what we think is possible and how we approach problems. While the success stories look like magic, getting these methods to work on a novel task often takes manual tuning, testing, and tweaking. Even after we get things working, most learning approaches for control have no guarantees of correct/desirable behavior.

My group focuses primarily on fundamental problems at the intersection of control systems and learning. We strive to characterize when algorithms work, how long they will take, and how much data is needed. Beyond math, we work with collaborators on applications including neural stimulation, aerospace control systems, soft robotics, and animal motion analysis. These applications keep us at least partially tethered to reality. (Just don’t make me build anything.)

One of my group's recent research streams is analyzing the behavior of variations of gradient descent, the backbone of calculations in much (if not most) work in machine learning. Specifically, stochastic gradient algorithms are typically employed to find a model that best explains the data. However, standard gradient methods can get stuck in local minima. That is, they can get stuck on models that are not as good as they could be. Work with my Ph.D. student Yuping Zheng examines how injecting random perturbations (i.e., noise) into gradient methods can help them out of a jam. (Figure 1.)

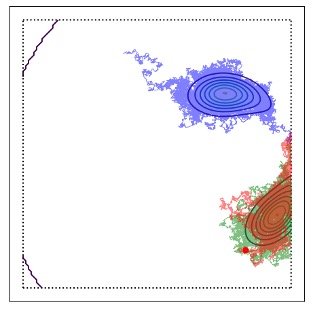
In particular, the noise can help push the models away from the local minima and help explore the space. Our work seeks to determine how much noise is useful and how long the resulting algorithms take to converge. Our specific contributions include analyzing the effects of constraints on the model parameters (commonly employed in practice but seldom analyzed) and examining their use in learning problems with dependencies over time (which is atypical of classical machine learning but common in systems and control). 

Another stream of research aims to characterize the behavior of control systems utilizing neural networks rigorously. One of the oldest and most successful uses of neural networks for control has been to capture the more complex phenomena that fall outside standard modeling techniques:

Model = (Known Physics) + (Complex Components, Modeled by Neural Networks)

For example, in a vehicle, many aspects of the model could be calculated from first-principles. Still, complex phenomena like wheel slips on rough terrain may not be so simple. In these cases, a neural network is often used to learn the behavior of these complex processes. Work with my Ph.D. student Tyler Lekang aims to determine when these neural networks can learn the required representations to do control. Our recent work gives theoretical justification for classical neural network initialization strategies that had been used for decades within controls but only had been analyzed in special cases.