Mind-bending Math
Posted October 2007
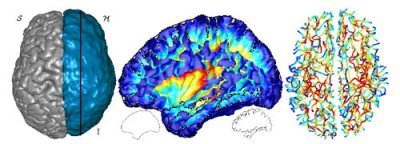
When viewed from the outside, a human brain appears as a volume with a highly wrinkled surface having numerous long crevices.
Sulcal fundi are 3D curves that lie in the depths of the cerebral cortex; informally, the fundus of a sulcus is the curve of maximal average depth that spans the length of the sulcus. The sulcal fundi serve as anatomical landmarks, `segmenting' the cortex into functionally distinct regions. They are often used as landmarks for downstream computations in brain imaging and can be used in creating deformation fields for warping the cortical surfaces of different brains onto one another.
Cortical sulci and sulcal fundi have traditionally been manually identified by labeling voxels in an MRI brain volume using a GUI that displays only three orthogonal 2D brain slices. This process is extremely tedious and time consuming and, not surprisingly, prone to human error. Given the large number of high resolution MRI datasets currently available for analysis, automatic and objective extraction and labeling of cortical sulci has become a necessity. IMA industrial postdoc Chiu Yen Kao and collaborators Michael Hofer (TU Vienna), Guillermo Sapiro (Minnesota), Josh Stern (Minnesota), and Daniel Rottenberg (University of Minnesota and VA Medical Center), have developed an automatic sulcal extraction method that promises to improve the quality and reproducibility of the process as well as yielding considerable time savings.
An outer hull surface is computed from a mesh representation of the graymatter (GM) surface by applying a morphological closing operation to the level set function. After the outer hull surface is obtained, the the geodesic depth (distance) for any given point on the pial surface to the outer hull surface is calculated. This results in the association of a sulcal depth estimate with each mesh triangle; the sulcal regions are determined using a depth threshold of 2.5mm. The connected components are identified using a labeling algorithm and the results are run through a thinning algorithm, yielding a skeleton of each connected component. The extracted sulcal fundi are represented as polylines that are further smoothed by an algorithm that minimizes a counterpart to the cubic spline energy for curves on surfaces.