3. Magnetic Anisotropy

The theory of ferro- and ferrimagnetism is based on electronic exchange forces. These forces are so strong that these material are spontaneously magnetized, even in the absence of an applied field. Yet, in the laboratory we need to apply magnetic fields to saturate a ferro- or ferrimagnetic material. In some cases, the material in bulk form has a remanence of nearly zero. This raises the question:

Why aren't all ferro- and ferrimagnetic materials magnetized to their saturated states, even in zero field?

To answer this question, it was postulated back in 1907, when the theory of ferromagnetism was first advanced, that ferromagnets are subdivided into many small subvolumes, called domains. Each domain is spontaneously magnetized to saturation, but the direction of magnetization varies from domain to domain. The net vector sum of all the domains therefore produce a total magnetization of near zero. It wasn't until the 1930's that domains were experimentally confirmed.

Before we study domains, we need to know a few facts about the influence of the crystal structure and the shape of grains on the direction of magnetization. The dependence of magnetic properties on a preferred direction is called magnetic anisotropy. There are several different types of anisotropy:

Type - depends on

1. magnetocrystalline- crystal structure

2. shape- grain shape

3. stress- applied or residual stresses

Magnetic anisotropy strongly affects the shape of hysteresis loops and controls the coercivity and remanence. Anisotropy is also of considerable practical importance because it is exploited in the design of most magnetic materials of commercial importance.

 

Magnetocrystalline Anisotropy

Magnetocrystalline anisotropy is an intrinsic property of a ferrimagnet, independent of grain size and shape. In can be most easily seen by measuring magnetization curves along different crystal directions.

For example, here are magnetization curves for magnetite.

Depending on the crystallographic orientation of the sample in the magnetic field, the magnetization reaches saturation in different fields.

In magnetite, above 130 K,

<111>  is the easy direction of magnetization

<100>  is the hard direction of magnetization

<110>  is the intermediate direction of magnetization.

For a sphere of magnetite there will be six easy directions of magnetization corresponding to the three [111] axes.

Magnetocrystalline anisotropy is the energy necessary to deflect the magnetic moment in a single crystal from the easy to the hard direction. The easy and hard directions arise from the interaction of the spin magnetic moment with the crystal lattice (spin-orbit coupling).

In cubic crystals, like magnetite, the magnetocrystalline anisotropy energy is given by a series expansion in terms of the angles between the direction of magnetization and the cube axes. It is sufficient to represent the anisotropy energy in an arbitrary direction by just the first two terms in the series expansion. These two terms each have an empirical constant associated with them called the first- and second order anisotropy constants, or K₁ and K₂, respectively.

At 300 K,

K₁ = -1.35x10⁵ ergs/cm³

K₂ = -0.44 x10⁵ ergs/cm³.

In hexagonal crystals, like hematite, the weak ferromagnetism lies in the basal plane, which is an easy plane of magnetization. The c-axis is the hard direction. It is extremely difficult to flip the magnetization out of the basal plan into the direction of the c-axis.

In these materials, saturation is usually never reached in fields normally used in the laboratory (1-2 Tesla). This behavior is useful to distinguish hematite from magnetite and other cubic magnetic minerals.

 

Stress Anisotropy

In addition to magnetocrystalline anisotropy, there is another effect related to spin-orbit coupling called magnetostriction. Magnetostriction arises from the strain dependence of the anisotropy constants. Upon magnetization, a previously demagnetized crystal experiences a strain that can be measured as a function of applied field along the principal crystallographic axes. A magnetic material will therefore change its dimension when magnetized.

The inverse effect, or the change of magnetization with stress also occurs. A uniaxial stress can produce a unique easy axis of magnetization if the stress is sufficient to overcome all other anisotropies. The magnitude of the stress anisotropy is described by two more empirical constants known as the magnetostriction constants (λ₁₁₁ and λ₁₀₀) and the level of stress.

 

Shape Anisotropy

The third type of anisotropy is due to the shape of a mineral grain. A magnetized body will produce magnetic charges or poles at the surface. This surface charge distribution, acting in isolation, is itself another source of a magnetic field, called the demagnetizing field. It is called the demagnetizing field because it acts in opposition to the magnetization that produces it.

 

For example, take a long thin needle shaped grain. The demagnetizing field will be less if the magnetization is along the long axis than if is along one of the short axes. This produces an easy axis of magnetization along the long axis. A sphere, on the other hand, has no shape anisotropy. The magnitude of shape anisotropy is dependent on the saturation magnetization.

For magnetite, smaller than about 20 microns, shape anisotropy is the dominant form of anisotropy. In larger sized particles, shape anisotropy is less important than magnetocrystalline anisotropy.  

For hematite, because the saturation magnetization is so low, shape anisotropy is usually never important.

 

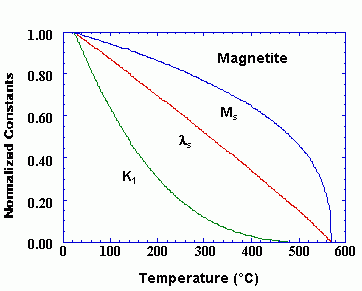
Temperature Dependence of Anisotropy

Both the magnetocrystalline and magnetostriction constants are dependent on temperature and particle sizes and the presence of impurity atoms seem to suppress these transitions, particularly for hematite.

For magnetite above room temperature, the magnetocrystalline and magnetostriction constants decrease with temperature and vanish at the Curie Temperature.