5. Thermally Activated Magnetizations
Néel [1949] developed a theory of remanence in SD particles based on thermal fluctuations. This model forms much of the theoretical basis for rock magnetism and provides a simple way of looking at the effects of time, temperature and field on the magnetization and demagnetization process.
Let's consider a collection of uniformly magnetized grains with uniaxial anisotropy in a magnetic field. The magnetization of each grain has only two stable magnetic states: parallel (+) or antiparallel (-) to the field. For a large number of identical, non-interacting grains, thermally activated transitions between the two stable states will produce an average equilibrium moment
Upon removal of the field, meq will decay exponentially to zero at a rate determined by a relaxation time. The relaxation time is proportional to the probability of transversing the energy barrier (EB) produced by the uniaxial anisotropy. In the presence of an external field the relaxation time is
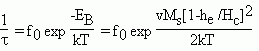
where Hc = coercivity Ms = saturation magnetization he = external field k = Boltzmann constant f0 = frequency constant
As stated before, grains having t much less than a typical experimental time t will reach equilibrium from any initial magnetic state during time t and will exhibit no remanence (superparamagnetic). Grains with t much greater than t will preserve the initial state after time t and their magnetization is effectively blocked. The blocking condition is determined at the point where t=t
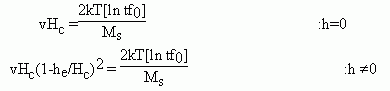
The blocking and unblocking equations can be described very succinctly on a Néel diagram. We have two cases:
case (i) he=0
The blocking equation is of the form
This equation describes an equilateral hyperbolae whose asymptotes are the v and Hc axes.
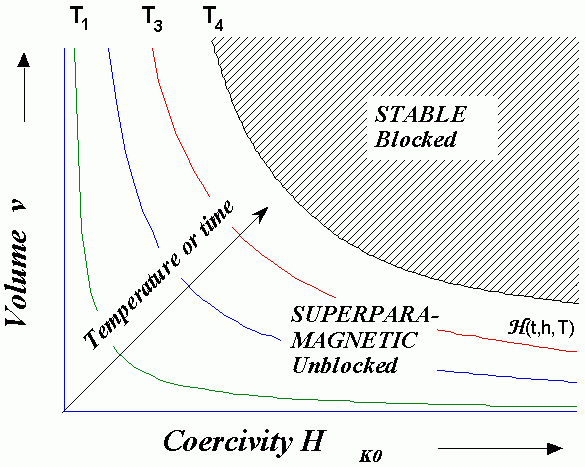
All points to the left of any curve H(t, he,T) correspond to grains with τ < t. Likewise, all points to the right have τ > t.
Grains with small v and Hc will be superparamagnetic. As temperature, or time, is increased, more and more grains with larger v and Hc will become progressively unblocked, until at T=TB when all grains become unblocked.
case (ii) he ≠ 0
When the field is not zero, the H(t,he,T) curves are asymptotic to the particular value of he
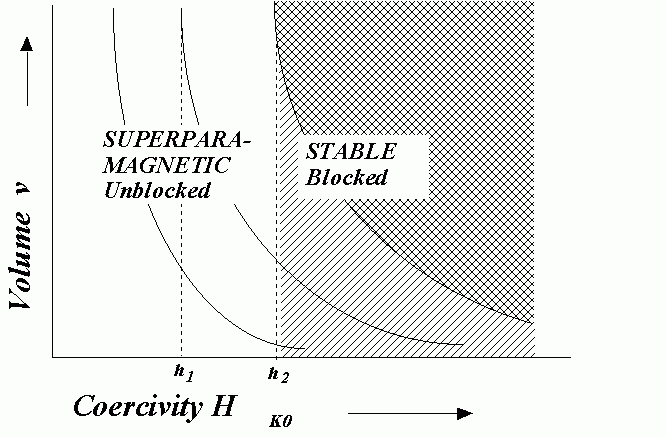
The motion of the blocking curves under the influence of h do not reproduce the motion due to temperature or time. Particles of small v and large Hc may require very large fields to become unblocked. However, the same grains can be unblocked by mild heating.
Demagnetization techniques
The above two cases of the Néel diagram provide the basis for selective demagnetization or magnetic "cleaning". The purpose of demagnetization is to remove the components of magnetization with short relaxation times which may contribute to secondary magnetizations that obscure the primary signal. Demagnetization is also useful for characterizing the coercivity distribution. There are two main methods:
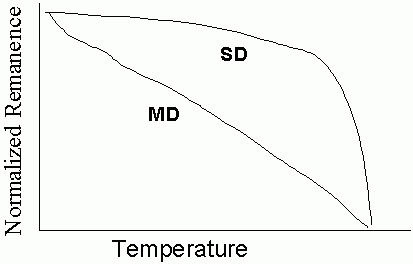
Thermal Demagnetization - A sample is heated and cooled in zero field for a series of increasing temperatures. After each step the remaining remanence is measured at room-temperature. Only those grains with blocking temperatures below the demagnetization temperature will be demagnetized.
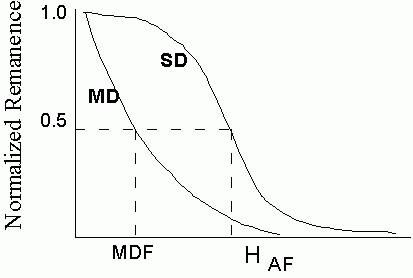
Alternating Field (AF) demagnetization - A sample is subjected to alternating field that is smoothly reduced to zero from some peak value. The AF demagnetization curve is measured by exposing the sample to a series of increasing AF peak values (5,10,15,20 ...100 mT). After each step the remaining remanence is measured. Remanence in grains with low coercivities are eased first. Remanence carried by grains with higher coercivities remains unaltered.
The AF value needed to reduce the initial remanence by one half is called the median destructive field, or MDF