Condensed Matter Theory Faculty
Fiona Burnell
Within the field of condensed matter theory, my primary research interest is in understanding phases of matter that are not described by the conventional Landau paradigm. My major contributions encompass a variety of questions ranging from the more mathematical problem of classifying topological and symmetry protected phases and their phase transitions, to empirically motivated questions such as how to detect topological superconductors and quantum spin liquids. More recently I have also become interested in the impacts of certain types of very strong correlations on quantum systems' dynamics and their ability to thermalize.
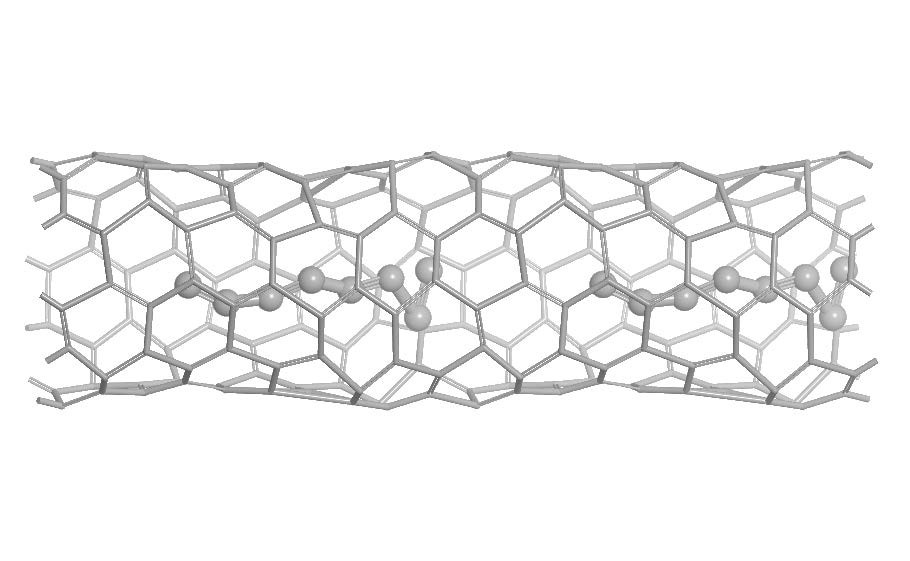
Below: In each layer of electron gas, electrons are visualized as composed of partons, each with a third of the electronic charge ee. The partons live in cyclotron orbits, whose number is a third of the cyclotron orbits of the electrons themselves. Under certain conditions partons can hop between layers, introducing an element of three dimensionality to a previously two-dimensional world.
Andrey Chubukov
My research interests are in the analysis of the role of orbital degrees of freedom in Fe-based superconductors, quantum-critical behavior and non-Fermi liquid transport in metals at the onset of charge of spin order, pairing in non-Fermi liquid regime in near-critical fermionic systems (e.g., systems at the verge of magnetic instability), and unconventional orders in frustrated antiferromagnets. In my research I combine analytical and numerical techniques. Methods include perturbation theory, parquet renormalization group, and Eliashberg theory (both for superconducting and normal state properties).
My research in the area of Fe-based superconductivity is chiefly focused at the moment on the role of orbital composition of low-energy excitations in Fe-based superconductors, on orbital scenario for nematicity in FeSe, and on thermodynamic properties of multi-orbital superconductors. Research on quantum critical behavior and non-Fermi liquid transport focuses on the structure of the propagator of critical bosons near a q=0 quantum phase transition in two dimensions, the role of vertex corrections for optical conductivity near a quantum critical point, and the structure of the dynamical susceptibility of a critical boson. My research on superconductivity near a quantum critical point is primarily focused on the problem of pairing of incoherent fermions due to the exchange of soft dynamic critical bosons and the role of fluctuations of the pairing gap. My research on frustrated magnets is primarily focused on the zero temperature phase diagram of a Heisenberg antiferromagnet on a frustrated triangular lattice in a magnetic field and unconventional spin-current states.
Rafael Fernandes
My main research interest is in the microscopic description of quantum materials. When a large number of electrons interact strongly with each other, as it is the case in many of these systems, they can behave very differently than how a single electron does. This gives rise to a variety of unusual and exotic behaviors, some of which have clear technological appeal, such as high-temperature superconductivity and quantum magnetism. Recently, I have been particularly interested in the collective behavior of electrons in a metal when a phase transition is driven all the way down to zero temperature, a phenomenon called quantum phase transition. I have also been investigating quantum states that are analogous to certain inhomogeneous patterns commonly observed in liquid crystals, such as electronic nematic phases.
Eric Ganz
I am interested in modeling the properties of novel materials. This can include 2 dimensional materials, as well as porous frameworks materials such as metal organic frameworks and covalent organic framework materials. These new porous materials are built from molecular building blocks, and so can be designed to provide a very wide range of capabilities. I use accurate ab initio density functional theory calculations at the supercomputer institute.
Woods Halley
Ongoing projects include studies of anomalous transmission through strongly interacting bose condensed liquids and quantum percolative models of superconductivity. I also continue some computational studies of electronic processes at electrochemical interfaces, mainly in consultation with groups in other laboratories and universities. Here I show results of a model calculation of electronic spectral density (which can be deduced from ARPES measurements) obtained from a percolative two dimensional tightbinding model containing point defects. This was a one electron calculation. The interest is that the result looks qualitatively similar to results from ARPES experiments on cuprate superconductors showing so-called 'fermi arcs' for which a variety of much more exotic explanations have been proposed. Self consistent mean field BCS calculations on a similar model (with full account of disorder) were reported by us decades ago and those calculations are currently being extended to a somewhat more realistic 3-band model.
Alex Kamenev
I work on a theoretical description of a wide variety of disordered and non-equilibrium systems. Over the years my research was focusing on nano-electrical circuits, cold atoms in optical traps, population dynamics, topological insulators and superconductors and lately models with gravity dual. I employ machinery of quantum field theory and other advanced chapters of mathematical physics to approach these problems. My group also has some experience in numerical simulations of systems at hand to aid the analytical progress.
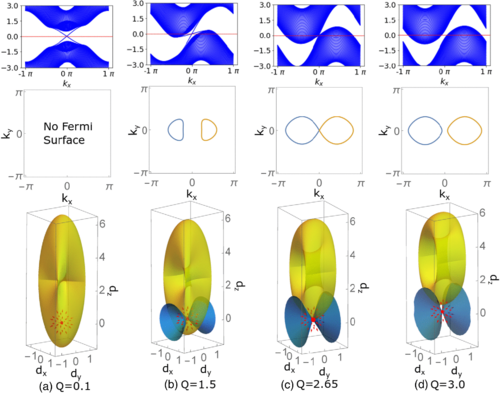
Left: The three rows show spectra as a function of kx, BZ with the Fermi surfaces, 3D dspace with the d(k) surface (gold), monopole at d=0 (red) and Fermi double cone, Eq. (7), (blue). The four columns correspond to different values of flux Q: (a) topological superconductor; (b) topological metal; (c) topological QPT; (d) ordinary metal. Figure 5specifies other parameters.
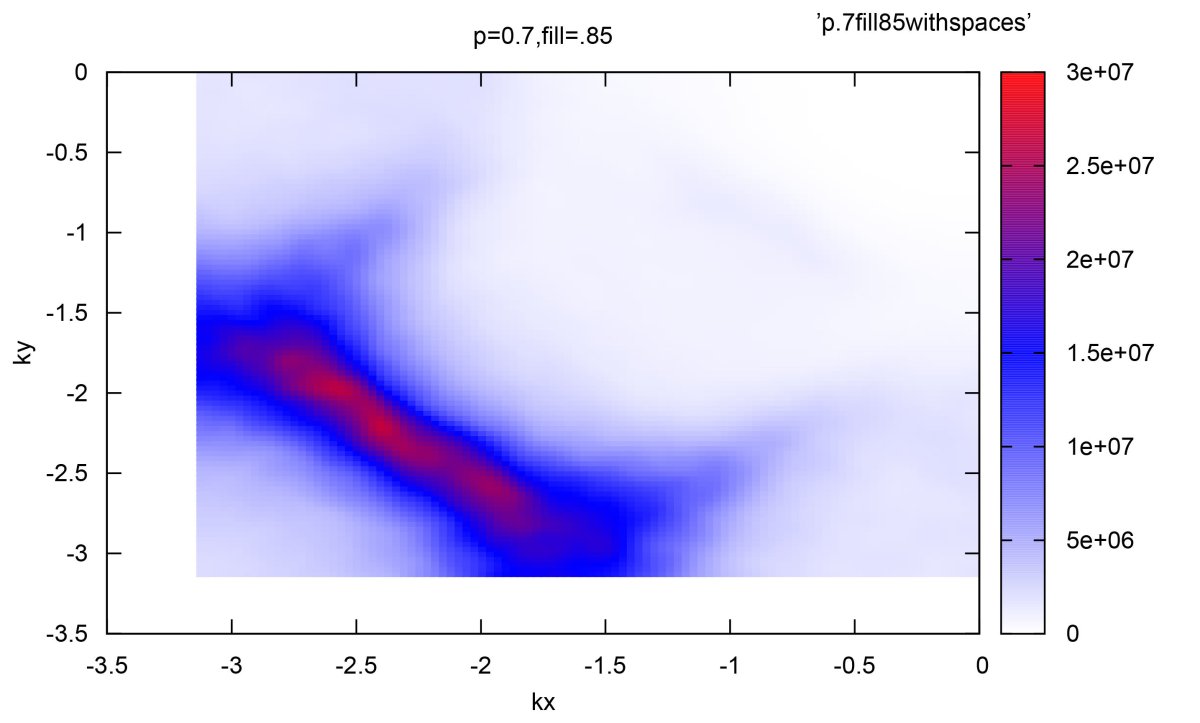
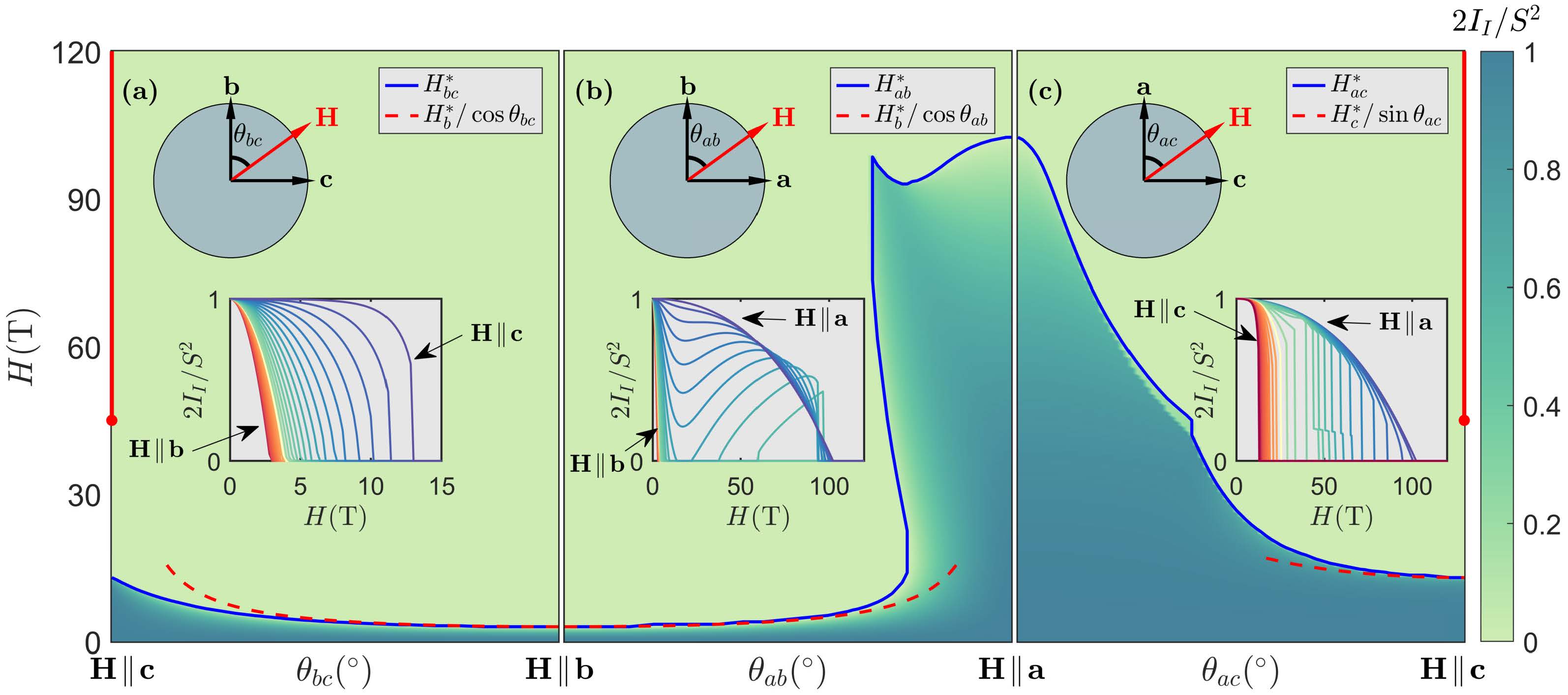
Natalia Perkins
Image caption: Ground state phase diagram of the Kitaev magnet beta-Li2IrO3 as a function of magnetic field strength H and its angular orientation in the bc plane (a), ab plane (b), and ac plane (c). The color coding tracks the evolution of the Bragg peak intensity of the modulated incommensurate magnetic order. More details in Phys. Rev. Research 2, 033328 (2020)
Boris Shklovskii
I study theoretically electric conductivity and electron mobility in different materials. They include bulk doped semiconductor crystals and films made of doped nanocrystals or metallic granules of several nm radius. I also study conductivity of two-dimensional electron gases (2DEGs) in AlGaAs heterojunctions, graphene and other 2D materials and concentrate on quality of integer and fractional quantum Hall effect. I also work on transport properties of 2DEGs in heterojunctions of different insulating perovskites such as LAO/STO and 2DEGs created in insulating crystals by gating with the help of ion liquids. Everywhere I focus on the role of the disorder and electron-electron interactions and try to understand how interplay between them leads to observed metal-insulator transitions.
Oriol T. Valls
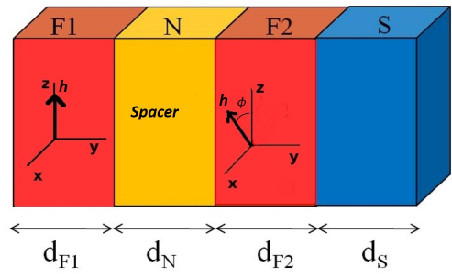
I study Superconducting and Magnetic Proximity Effects in F/S nanostructures; Exotic forms of superconductivity; Charge and Spin Transport in F/S nanostructures; Superfluid Hydrodynamics; Dynamics of quantum Crystals.
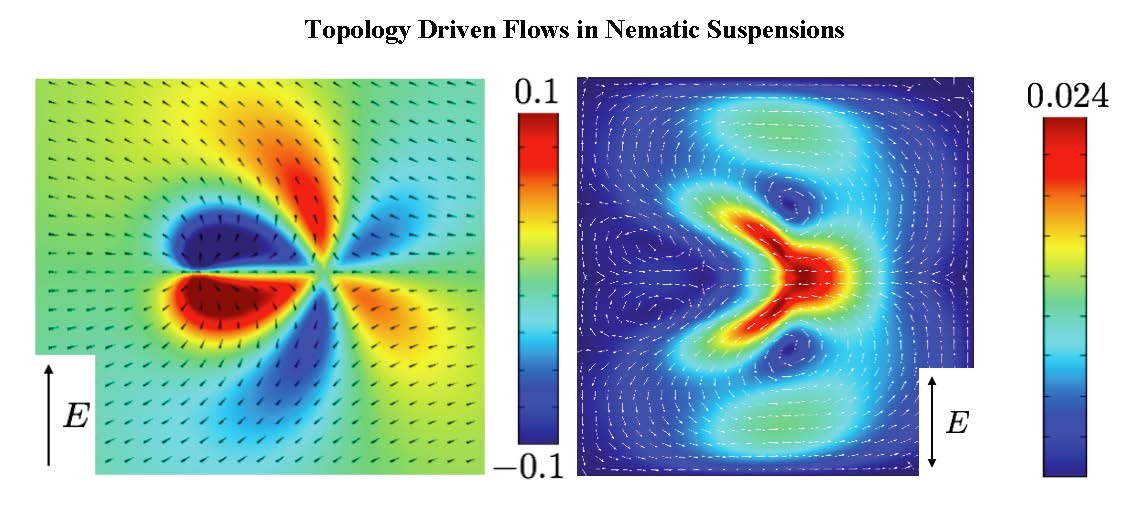
Jorge Viñals
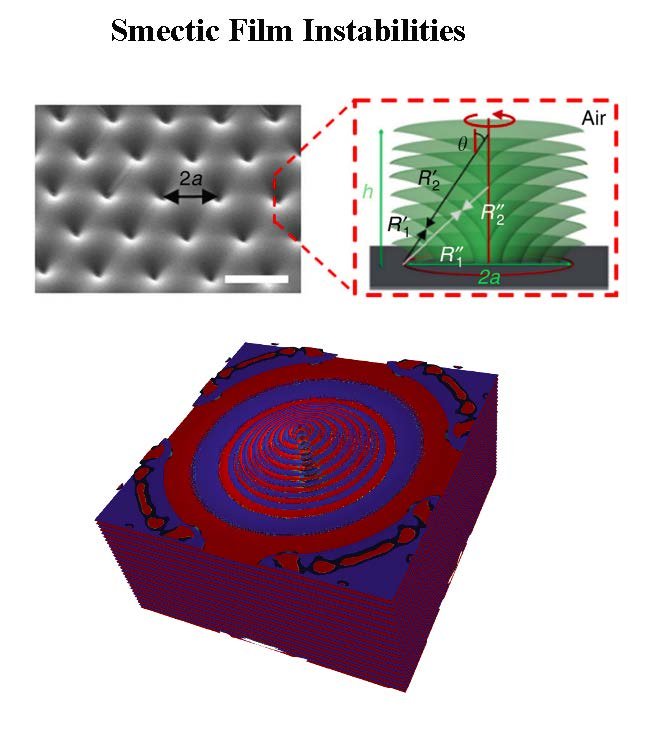
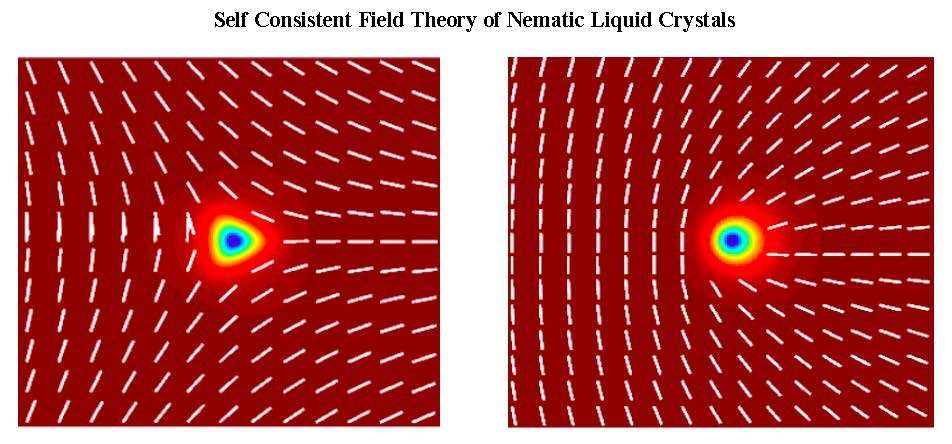
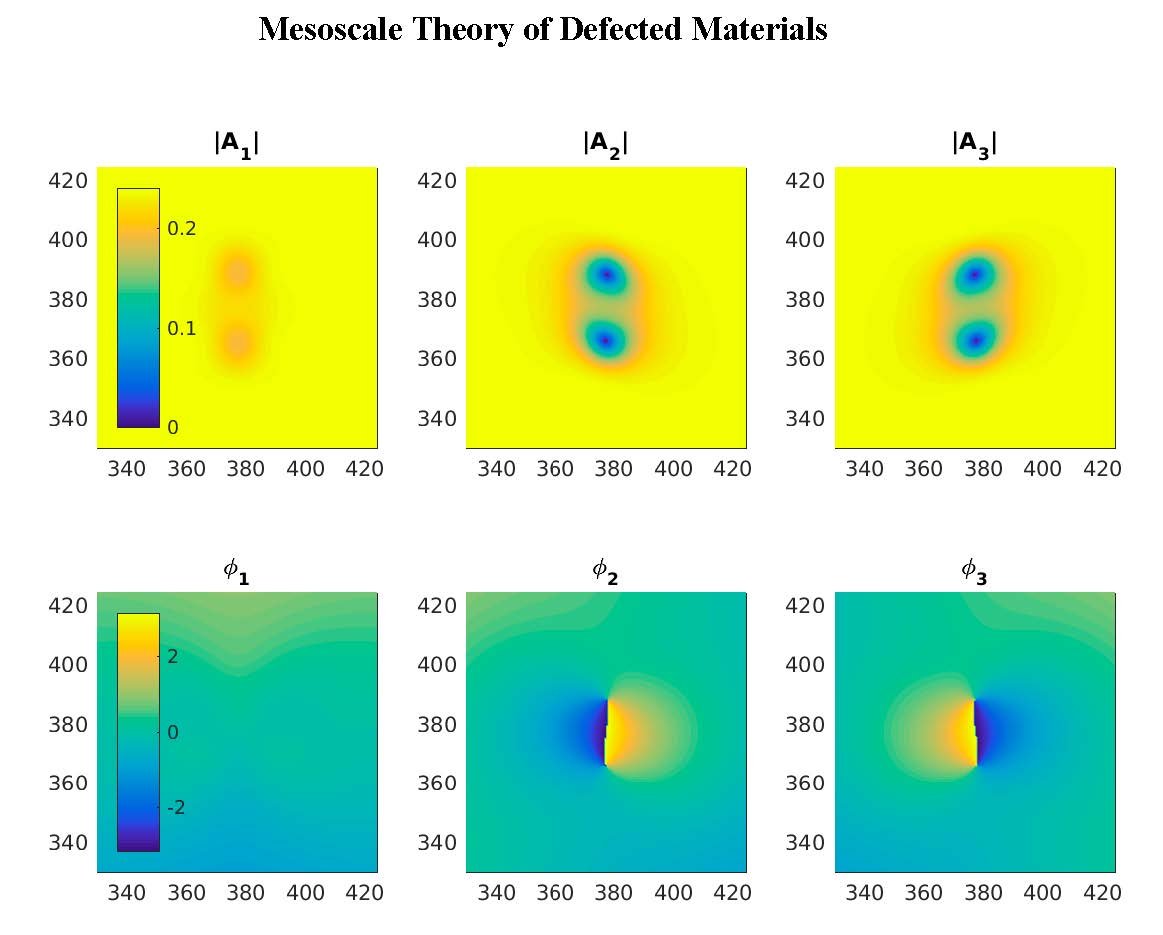
Our research is of theoretical and computational nature, and focuses on mesoscale theories of nonequilibrium phenomena in extended systems, with applications to Statistical Mechanics, Soft Matter Physics, and Materials Science. Generically, systems outside of thermodynamic equilibrium involve unstable interfaces and moving topological defects. We develop theories at the mesoscale of the relevant phases, analyze their macroscopic scale asymptotics, and obtain their non equilibrium properties through large scale computation. Our research is currently motivated by topologically driven flows in liquid crystals, unstable interfaces in complex fluids, and a mesoscale description of plasticity in defected materials.
Research is currently being done in these four areas:
Emeriti
Charles E. Campbell (Emeritus)
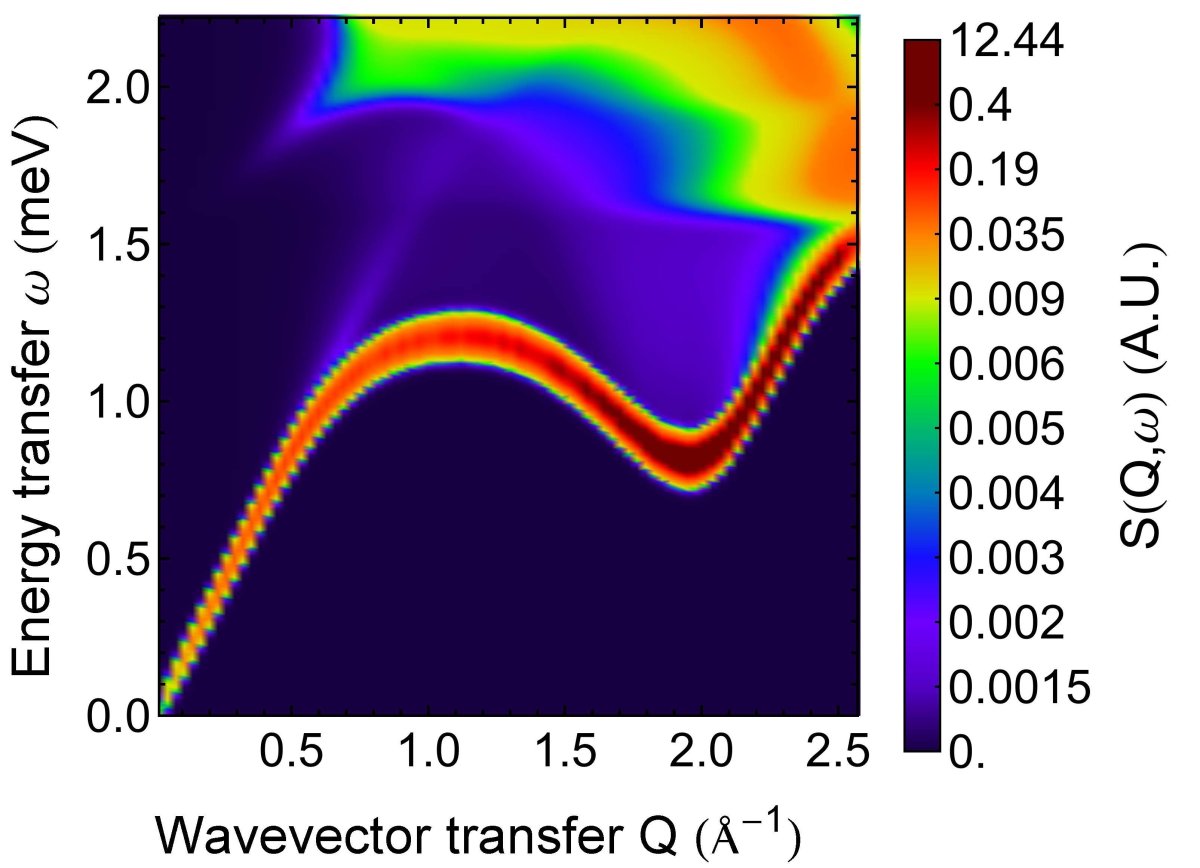
My primary research is on the ab initio many-body theory and statistical mechanics of very strongly correlated quantum fluids. This includes the helium fluids, low density electron many-body systems and low density quantum plasmas, all of which have properties that cannot be well described by traditional quantum many-body theories such as mean field, Landau theory, density functional theory, or dynamic mean field theory. The challenges are due to the very strong correlations between the particles in these systems. To understand the consequences of these strong correlations, we have been heavily involved in the development of Dynamic Many-Body Theory, which recently has been highly successful in accounting exceedingly well for inelastic neutron scattering from superfluid liquid helium four. This theory and these experiments have revealed a much richer multi-quasiparticle dynamics than previously known. The experiments have been near absolute zero and the theory at absolute zero. We are continuing our work to extend the theory to finite temperature, including the phase transition from a normal fluid to a superfluid in liquid helium four.