A Paradigm-changing Framework for Reliability-based Analysis and Design of Concrete Structures: Jia-Liang Le

No engineering structure remains risk-free during its entire service lifetime. Engineers must design structures to limit probable risk of failure to a tolerable level. Because of many of the factors affecting the risk of failure, probabilistic methods have become an indispensable tool for structural design.
For concrete infrastructure (for example, buildings, bridges, dams) the acceptable risk of failure is typically one in one million, or even lower. Ensuring such a low risk poses two unique challenges when designing and analyzing concrete structure: 1) Determining such a low probability of structural failure would require repeating experiments or numerical simulations at least one hundred million times, and 2) Design extrapolation is required because, in many cases, the actual structures are much larger than laboratory test specimens.
Le and his research team recently developed a finite weakest-link model to analyze strength statistics of concrete structures. The underlying concept of the weakest-link model is that a structure is only as strong as its weakest element.
The structure's peak load capacity is reached if one material element is fully damaged. Therefore, a structure can be statistically modeled using a "chain" of material elements. The established practice is to use an infinite weakest-link model, which assumes that there are an infinite number of material elements in this chain. In contrast, the new finite weakest-link model acknowledges that in concrete structures, material elements have a finite size, and that size may not be negligible compared to the characteristic dimensions of the structure.
By explicitly introducing the size of a failing material element, the finite weakest-link model is able to capture the effect of that element size on the probability distribution of the structural strength. The new model predicts that the probability distribution of structural strength will transition from a predominantly Gaussian distribution to a Weibull distribution as the structure size increases (Figure 1). As a result, the conventional infinite weakest-link model (which leads to the Weibull strength distribution) becomes a limiting case of this general model for large-size structures.
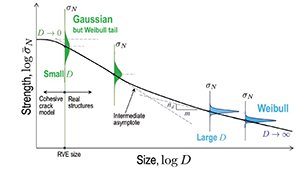
The size dependence of strength distribution directly leads to an intricate size effect on the mean strength of the structure, which predicts that large structures will be weaker than small structures (Figure 1). This phenomenon can be explained by the fact that a large structure likely contains more weak spots compared to a small structure, and the strength of the structure is determined by the strength of the weakest spot. Therefore the average failure stress of a large structure would be smaller than that of a small structure.
Such a statistical size effect was first speculated by Leonardo da Vinci in 1500s, and qualitatively explained by Edem Mariotte in 1686. In 1939, Weibull proposed a mathematical model for describing such a size effect (aptly called the Weibull size effect) based on the concept of infinite weakest-link model. Abundant experiments have show that the Weibull size effect is not applicable to concrete structures because it does not account for the finite size of the failing material element. By overcoming this limitation, the new finite-weakest link model leads to a more general mean size effect curve that is applicable to concrete structures of any size.
Based on the finite weakest-link model, Le and his team further derived an analytical redistribution and the strength distribution and the size effect on mean strength. This analytical relationship offered the researchers a new experimental method for determining the probability distribution of structural strength based on mean size effect analysis. Their new method is far more efficient than the conventional histogram testing method for determining strength distribution because it requires fewer specimens and repetitions and the result is less affected by the experimental error.
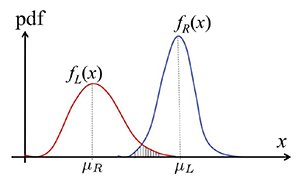
Le and his research group also directed their efforts to combining the finite weakest-link model with existing methods of reliability-based structural design of concrete structures. The central safety factor engineers use to guarantee a tolerable risk of failure is the ratio between the average load capacity (how much a structure can bear) of a structure and the average applied load (how much a structure is asked to bear). Therefore the safety factor can be determined such that the probability density curves (curves describing the capacity and the applied load of a structure) will overlap only a small amount (Figure 2). Since the finite weakest-link model predicts a strong size effect on the probability distribution of structural strength, it is expected that in order to guarantee a prescribed level of failure risk, the safety factor must be dependent on the structure size. Le and his group proposed approximate equations for such a size effect by using asymptotic analysis.
CASE STUDY

As a case study, Le and his team recently applied the finite weakest-link model to re-analyze the failure of the ill-fated Malpasset Dam (Figure 3). The dam was built across the canyon of the Reyran Valley in France in 1954, and it failed in 1959 the first time the reservoir was filled to capacity (after 5 days of heavy rain). It was generally accepted that the failure was due to the development of vertical flexural cracks engendered by the lateral displacement of the abutment. In their re-analysis, Le and his students used a simplified 2D arch model to represent the mid-height cross-section of the dam. To study the size effect on structural reliability, they considered a set of geometrically similar arches (Figure 4), the smallest size being a laboratory test specimen and the largest size being the actual Malpasset Dam.
The analysis indicated that direct extrapolation of laboratory-scale test results to full-scale design without the consideration of size effect would result in a failure risk 1000 time greater than the tolerable level (Figure 5). To ensure a prescribed failure risk for structures of different sizes and geometries, designers must consider size effect on safety factors.
Existing design approaches assume safety factor to be a constant, regardless of structure size and geometry. The new finite weakest-link model could potentially lead to a paradigm change in design practices.
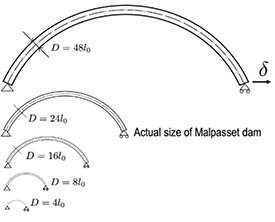
Figure 4. Size effect analysis of a set of geometrically similar arches. |

Figure 5. Direct extrapolation of laboratory tests to full scale design will result in a significant increase in failure risk of the actual structure. |
LE RECEIVES 2017 EMI LEONARDO DA VINCI AWARD
Associate Professor Jia-Liang Le has been selected as the recipient of the 2017 EMI Leonardo da Vinci Award. The Engineering Mechanics Institute (EMI) of the American Society for Engineering presents this award to recognize outstanding young investigators (under 35 years of age) for promising ground-breaking developments in the field of Engineering Mechanics and Mechanical Sciences as relevant to Civil Engineering.
The overarching goal of Le's research is to improve the resilience of civil engineering structures through advancing the fundamental understanding of probabilistic failure of quasibrittle materials. Le's expertise uniquely centers at the intersection of fracture mechanics, probabilistic methods, and computations mechanics, which has led to several important results that represent a new paradigm of the analysis and design of structures. The award will be presented at the EMI 2017 Conference in June.