What would you do if you had 10, 1,000, or 10,000 robots?

If you had a bunch of tasks to accomplish and you could use robots, how many robots would you use? Does the answer depend on the tasks? Are the tasks independent of each other, so they can be done in parallel with no coordination, or do they have precedence or temporal constraints? Do the robots need a central controller to coordinate their work, or could each robot work independently? Who will decide which robot does what task? These are central questions that have been addressed in the work of Professor Maria Gini's research group.
Task allocation to robots
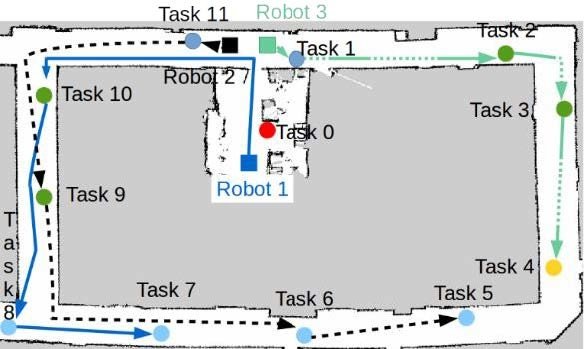
Gini and her research team have worked on a class of task assignment problems where there are constraints on when, where, and in what order tasks need to be executed. They have defined this class of problems, which they call Multi-robot Task Allocation with Temporal and Ordering Constraints (MRTA/TOC) and examined the approaches that have been taken to address it [1].
For scalability and robustness reasons, they have focused their work on decentralized approaches, where the allocation of tasks is done using auctions. Robots bid on tasks based on the amount of effort they need to complete each task or the amount of time it will take to do them. They have proposed the Temporal Sequential Single-Item auction (TeSSI) algorithm [2], which uses as the main cost function the makespan (i.e., the time the last robot finishes its final task). Each robot maintains the schedule for the tasks assigned to it. Before bidding on a new task, each robot finds the optimal place in its schedule for that task and uses the makespan of the resulting schedule for its bid.
The algorithm supports both offline allocation of tasks, when all the tasks are known upfront, and online allocation, when tasks arrive dynamically. The algorithm has been tested in simulation on multiple problems with up to 100 tasks and up to 50 robots in different environments, both indoors and outdoors [2]. The researchers have extended TeSSI to include ordering constraints in addition to temporal constraints and studied how to model risks in the schedule caused by uncertainty about the time needed to execute the tasks [6].
Swarm robotics
What if there were many more robots, in the order of 1,000 or more? At very large scales, different types of algorithms are needed. Here is where swarm robotics gets into the picture. Swarm robotics aims at using many simple robots to do the tasks. The inspiration comes from nature, in particular insects like ants, bees, and termites that can accomplish complex tasks, such as food collection or nest construction, by contributing individually to the task. There are many reasons why this approach looks intriguing. After all, if small insects can do complex tasks, robots should be able to do the same.
Swarms of robots have four main valuable properties: scalability, emergent self-organization, flexibility, and robustness. Gini's team has studied how to measure precisely these properties and use them to provide ways to predict the behavior of a swarm of robots without having to run extensive simulations but using the mathematical characterization of their properties [4, 5].
To measure scalability, they compute how much of the observed behavior is due to robots cooperating as opposed to avoiding running into each other. To measure emergent self-organization, they measure if doubling the swarm size in a confined space results in doubling the inter-robot interference when robots are moving randomly. Sub-linear increases in interference indicate self-organization. Third, to measure flexibility, the team compares swarm performance in changing environmental conditions to ideal conditions to quantify the ability of the swarm to adapt to changes. Finally, to measure robustness, the swarm is modeled as a queue and the rates at which robots enter/leave the queue when they malfunction are used to measure the consistency of swarm performance despite changes in the swarm size.
The traditional task studied for swarms of robots is foraging, which can be used to study real world tasks, such as search and rescue, warehouse transport of objects, garbage collection, and exploration. The group has studied how giving the robots the ability to decide how to decompose the foraging task can produce performance improvements [6]. In this case, instead of collecting food and bringing it directly to the nest, robots can partition themselves into “gatherers” and “collectors” and create one or more temporary locations to where gatherers will drop the food and the collectors will take it from there to the nest. The researchers have also studied how to compute the distribution of the “first passage time”, which is the first time when a robot doing correlated random walk reaches a specific location, in this case the nest area, and have extended the results, with some additional assumptions, to multiple robots [7].